** Exercice de synthèse

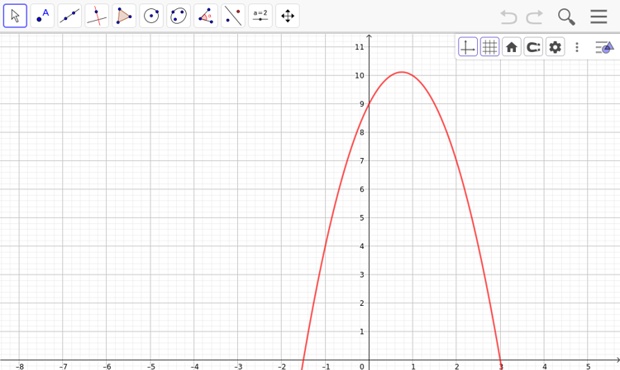
Soit \(f\) la fonction définie sur \(\mathbb{R}\) par \(f(x)=-2x^2+3x+9\), dont on donne la courbe représentative \(\mathscr{C}\) ci-dessous, dans un repère orthogonal du plan.

On considère la fonction affine \(g\) telle que \(g(1)=2\) et \(g(-2)=5\).

1. Démontrer que, pour tout réel \(x\), on a \(g(x)=3-x\).

2. On note \(D\) la représentation graphique de la fonction \(g\). Soit A et B deux points appartenant à la droite \(D\). Tracer la droite \(D\) dans la graphique ci-dessus.

3. Par lecture graphique, déterminer l'ensemble des solutions de l'inéquation \(f(x)\geqslant g(x)\).

4. Démontrer que, pour tout réel \(x\), on a \(f(x)=(2x+3)(3-x)\).

5. Pour tout réel \(x\), on pose \(h(x)=f(x)-g(x)\).
    a. Démontrer que, pour tout réel \(x\), on a \(h(x)=2(x+1)(3-x)\).
    b. Résoudre dans \(\mathbb{R}\) l'inéquation \(h(x)\geqslant 0\).
    c. Ce résultat était-il prévisible ?